merge-insertion sort, 혹은 Ford–Johnson algorithm 찬찬히 뜯어보기(2)

이전 글 보러가기 : 

https://ebang.tistory.com/103

 

 

3. merge insert sort

그래서 결국 merge insert 는 뭔가하면,
배열을 쪼개고 다시 합병하는 과정이라는 점에서 merge sort, 
원소가 들어가는 부분을 탐색하는 점에서 Insertion sort 의 포인트를 갖고 있는 알고리즘이라고 할 수 있다.
단 이전의 insertion sort 에서 설명된 것과는 다르게 삽입될 부분이 이진탐색으로 탐색된다. 
이진 탐색은 이미 배열이 정렬되어있을 때, 특정 값이 들어갈 위치를 범위를 절반으로 줄여가면서 탐색하는 기법이다. (중간값보다 크면 그 이후 범위에서 다시 찾고, 중간값보다 작으면 그 이전 범위에서 다시 찾는 방식)
 

 그리고 이게 핵심이다. binary search에 소요되는 탐색 수를 줄일 수 있는 방법을 적용했기 때문에 가장 적은 비교 횟수로 비교하는, 
 즉 Minimum-Comparison Sorting algorithm에 속하게 되었기 때문이다. 
 
 
 
 
 
우선 방법은 다음과 같다. 
예시로 [11 7 5 3 20 22 ] 이 있다고 하자. 
 
1. 배열을 이루는 모든 원소들을 한 쌍씩 묶어서 더 큰 원소가 앞에 오도록 정렬한다.  홀수개의 배열이라면 마지막 원소는 남겨둔다.
[11 7] [5 3] [22 20]
(각 쌍에서 주황색 >= 파란색)

2. 각 쌍의 앞에 위치한 더 큰 원소를 기준으로 정렬한다. 
[5 3] [11 7] [22 20]
(주황색을 기준으로 정렬된 상태.)

 

 
3. 앞에 위치한 더 큰 원소들을 mainChain 이라고 부르고, 나머지 원소들을 pendingElements 라고 부르자. 
또한 mainChain 원소들은 a1, a2, a3... 이고 pendingElements는 b1, b2, b3... 라고 하자. 

그럼 다음과 같은 상태가 된다.

 

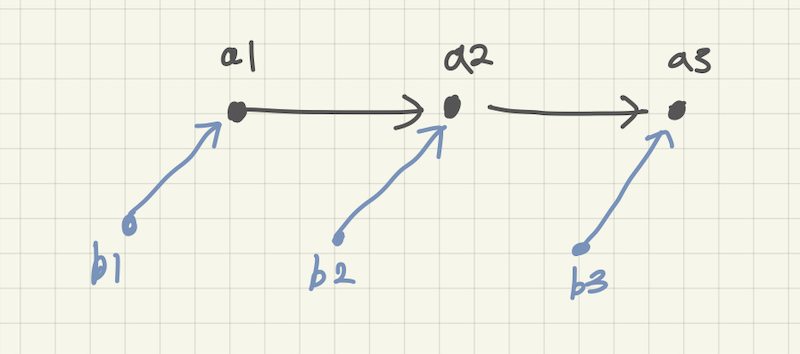
mainChain : {5 , 11, 22 } = {a1, a2, a3}
pendingElements = {3, 7, 20} = {b1, b2, b3}
 
4. mainChain에 속한 ak 원소들은 모두 정렬되어있는 상태이고,  bk들을 mainChain의 어디에 삽입할 지를 정한다. (insertion)
 이때 bk를  단순히 b1부터 차례로 b1, b2, b3.... 순서대로 mainChain에 삽입될 위치를 찾는 것이 아니다. 
 
5. 첫번째로는 b1의 위치를 정한다. 
b1 < a1 이므로  (1번에 의해 bk < ak 가 성립함.) 무조건 b1은 a1 앞에 온다.
mainChain : {3, 5 , 11, 22} = {b1, a1, a2 a3}
pendingElements = { 7, 20} = {b2, b3}

 
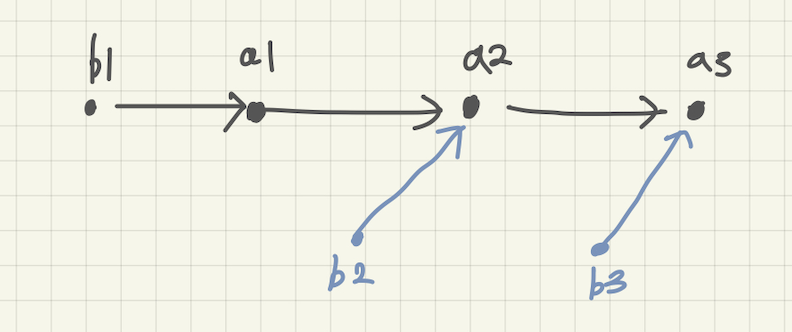
6. 두번째로는 b3의 위치를 정한다. 
{b1, a1, a2}  중 위치할 곳을 찾는다.  (b3 < a3 이므로. )이진탐색을 이용해서 찾는다. 
이 경우 21보다 크므로, 
mainChain : {3, 5,  11 , 20, 22} = {b1, a1,  a2, b3, a3}
pendingElements = {7} = {b2}

 
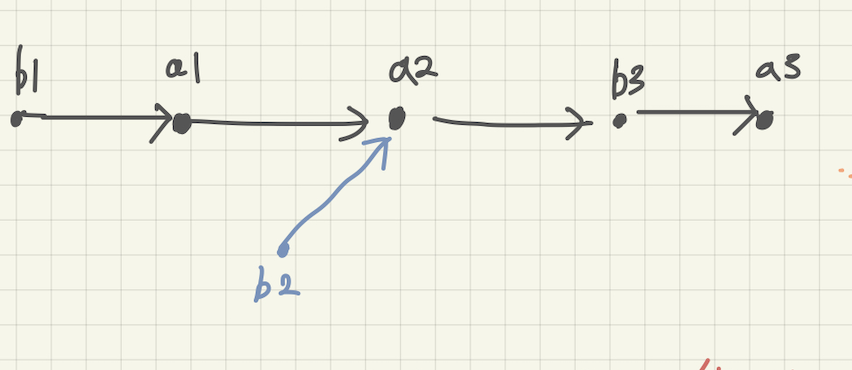
7. 세번째로 b2의 위치를 찾는다. 
 b1 < a1 < a2< a3 이고 b2 < a2이므로, b2가 속할 수 있는 구간은  {b1, a1, a1} 이다.  ({3, 5, 11} 구간)

이 구간에서 b2가 속할 수 있는 곳을 찾으면 
mainChain : {3, 5, 7, 11 , 20, 22} = {b1, a1, b2, a2, b3, a3}
pendingElements = {}
 
이렇게 정렬이 끝난다. 
 
 

왜 b3를 b2보다 먼저 삽입정렬에 이용했을까? 

case.1) 6번에서 b3를 삽입할 위치를 찾는 시점은, {b1 a1 a2 a3} 중에서 b3 < a3 이므로
{🛑b1🛑 a1🛑 a2🛑} 중 한 자리에 b3가 위치할 가능성이 있을 때였다. 
이때 b3의 위치를 찾기 위해 이진탐색을 할 때, 최악의 경우 탐색의 횟수는 2번이다.
 
case.2)  반대로 b2를 먼저 삽입했다고 생각해보자. 
{3 5 7 11 20 22} = {b1 a1 b2 a2 a3} 이고 
 {🛑b1 🛑a1 🛑b2 🛑a2🛑}  중 한자리에 b3가 위치할 가능성이 있고, 
이진탐색을 할 때 최악의 경우 탐색의 횟수는 3번이다.
 
case 1 처럼 b3를 먼저하고 b2의 위치를 탐색한다고 할 때,  b2 < a2 인 상황이므로, a2가 어디에 있든지 무시하고 
{🛑b1🛑 a1🛑 b3🛑}  이 상황에서 b2의 위치를 탐색할 수 있다.  즉 탐색 횟수가 최적화되는 것이다. 
 

 

그림으로 정리하면 다음과 같다. 

 

 

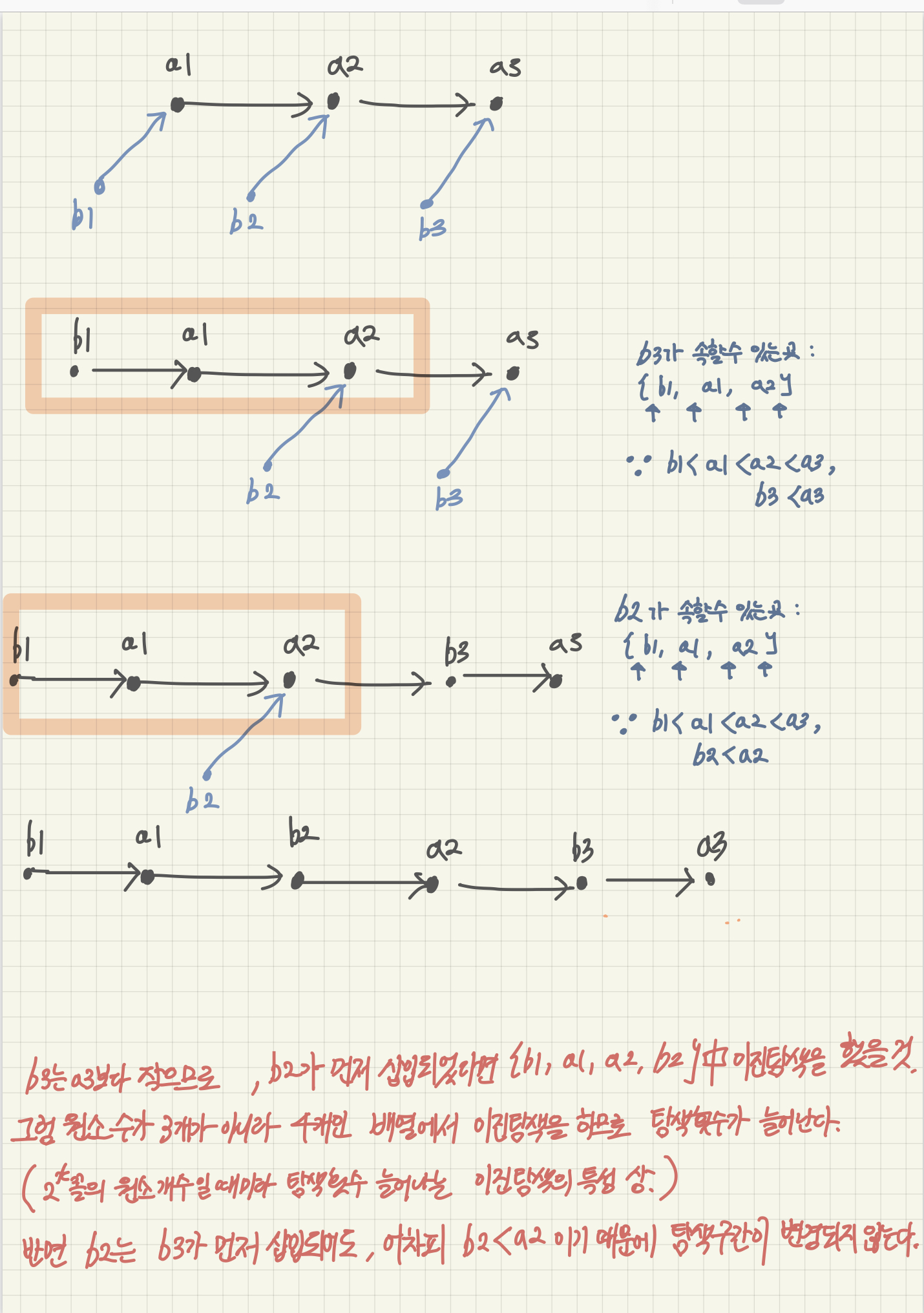
물론 b3가 항상 저 위치에 삽입되는 건 아니기 때문에,  a1, a2 사이에 b3가 있었다면 탐색횟수는 이득이 없었을 것이다. a2의 탐색 구간 개수가 {b1, a1, b3, a2 }로 늘어났을 것이므로....  하지만 저런 상황에서는 이진탐색을 하는 횟수가 줄어들기 때문에, 그런 상황들에 맞춰서 '운이 좋다면' 탐색횟수를 줄일 수 있는 알고리즘이 탄생할 수 있는 것이다.  답답하게도 알고리즘을 소개할 떄는 이게 이런 상황에 의존한다는 말이 없어서 긴가민가 한 게 이해하는데 가장 방해되었다. 
 
아무튼 그림을 보면 거의 다 이해했을 것이다. 

 

이제는 좀 더 수식적으로 정리해보자. 
핵심은 배열을 쪼개서 Insertion을 통해 merge를 하고, insertion 에선 이진탐색으로 insert 할 곳을 탐색하는데,
이 탐색 횟수가 가장 최소화 될 수 있는 방향으로 순서를 진행한다는 것이다. 
 
이때 bk의 인덱스 값은

Jacobsthal number 를 따른다.

이 수는 다음과 같은 규칙을 따르는 수이다. (값 :0, 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365.. )
이 값에 의해서 정렬되는 원소의 순서가 (1, (3,2), (5,4), (11, 10, 9, 8, ,7, 6) (21, ...) ) 이렇게 된다.
 
 

 

 

 

즉 merge-insertion 정렬은 주어진 요소들을 두 개씩 비교하고, merge sort를 사용하여 더 큰 요소들을 정렬하는 과정을 거친다. 이로써 주 연결 리스트(mainChain)가 형성되고, 이진 탐색을 통해 요소를 주 연결 리스트에 삽입한다.
이 그림에서  총 21개의 원소가 있을 때, 
윗 줄이 처음 정렬된 mainChain 이고, 아랫줄이 아직 정렬이 안된, 그러나 ak > bk는 만족하는 bk의 모습이다.
(사족을 붙이자면 b11은 떨어져있다 .홀수라서)
 

 
 

그럼 왜 Jacobsthal number를 따르게 되었나?

이진탐색에 대해 알아볼 시간이다.
이진탐색은 정렬된 배열 또는 리스트에서 특정 값을 찾는 알고리즘으로, 중간 값을 선택하고 찾고자 하는 값과 비교하여 탐색 범위를 반으로 줄여가는 과정을 반복한다. 
 
이때 탐색 범위를 반으로 줄여간다는 점에서, 원소의 개수가 2^K 일 때부터 2 ^(K + 1) -1 개일 때 탐색 횟수가 동일하다.  k번으로 동일하다.
(원소의 수가 2배가 될 때마다 최악의 경우 탐색해야하는 횟수가 늘어난다는 뜻.)
 
원소의 수가 2개일 때는 3개일 때와, 원소의 수가 4개일 때는 5,6,7개일 때와, 원소의 수가 8개일 때는 9 ,... 15개일 때와 탐색횟수가 같다는 뜻이다.
 
탐색 횟수가 1번인 원소 수 = 2, 3 (2개가 동일)
탐색 횟수가 2번인 원소 수 = 4,5,6,7 (4개가 동일)
탐색 횟수가 3번인 원소 수 = 8,9,10,11, ... 15 (8개가 동일)
탐색 횟수가 4번인 원소 수 = 16, 17, ... 31(16개가 동일)
... 이다. 
 

 
tk 라는 점화식을 쓸거다 .
아래 첨자가 안되는 만큼 그림을 참고해서 k를 t의 아래첨자로 주의깊게 봐주길 바랍니다..
 
 
아래 그림 처럼 b의 t(k-1)+1 인덱스부터 b의 t(k) -1번까지 추가할 때까지 binary search 하는 횟수가 같다고 치자.  
그렇다고 가정해서 tk에 대한 식을 구한 후,  그만큼을 mainChain에 삽입정렬할 것이다. 
쉽게 말하면 최악의 경우 탐색 횟수가 (k-1)회인 전체 탐색 원소수의 최대 = 2^(k) -1 개가 될 때가 t(k)의 값이다.  

t(k) : 그 이전까지의 인덱스를 모두 추가하면 전체 원소 개수가 이진탐색시 최악의 탐색횟수가 k-1회가 되는 인덱스.  말이 어렵지만 잘 이해하면 거의 다 따라온거다

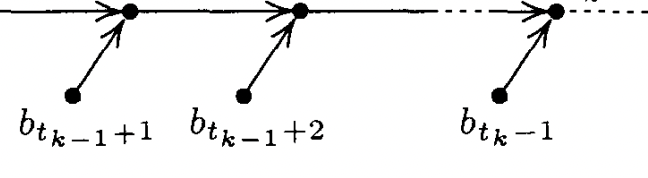
이때 mainChain의 전체 탐색대상의 원소의 수부터 살펴보자.
 bi < ai 이므로 그 이전까지가 탐색대상이다.
따라서 a(tk) -1 까지  포함해서 계산해야하고, 
그 개수는 다음과 같다.
(bt(k-1)에 도달하기까지의 추가된 원소수 (b1 ~ bt(k-1), 위위 그림에서 x) + a수열의 개수(a1~ a(t(k-1)) + (실제로 더해진 b수열의 개수(t(k) - (t -k(k-1) -1 ))

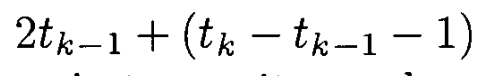
그리고 이 전체 탐색 원소수 = 2^(k) -1 개가 될 때가 tk의 값이다.  (다시한번 말하지만 binary search 하는 횟수가 동일할 떄까지.)
즉 이 두 식이 위 아래가 같을 때다. 
 

 
 
 
 

 =

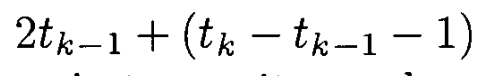
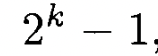
이 식을 정리하면 

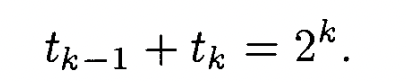
이런식이 나온다. 
 
즉 우리는 k번째에서 b 수열의 인덱스는 t(k-1) 부터 t(k) -1까지 추가할 건데,  그 tk는 위의 식을 따른다.
그리고 tk 가 바로 Jacobsthal number 이다. 
 

여기 점화식중 가장 마지막을 보면 Jn+1 = 2 ^ n - Jn 이게 위에서 도출한 tk와 비슷한 식인 것이 보인다.  
 
그니까 b의 인덱스가 Jacobsthal 식을 따르고, J(k-1)+1 ~ J(k-1) 까지의 인덱스를 삽입정렬하는 식이라고 이해하면 된다. 
 
위 사항을 잘 이해하고 싶다면, 이진탐색에 대한 깊은 이해와 더불어서
mainChain에  pending Elements가 추가되는 과정을 직접 해보길 바란다. 위의 예시를 직접 손으로 그려가면서 해보면 훨씬 나을거다. 
 
 

직관적으로 이해하기

직관적으로 이해하려면 이런 식의 사고가 더 도움이 된다.
 
bn 이라는 값은 그 이전 b(n-1)이 정렬된 후로부터 binary search 하려는 횟수가 동일한 최대의 값이다. 
(b(n-1) + 1, b(n-1) + 2, b(n-1) + 3, ... b(n) 까지는 insertion 하는 동안 binary search 횟수가 동일하다. )
 
대강 bn이 따르는 Jacobsthal number 를 보면 이제 두번째 식을 잘 봐보자.

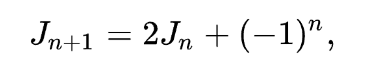
이전의 값에서 2배를 해준 후 1을 빼거나 1을 더한 값이다.
이진탐색의 횟수가 늘어나는 경우 역시 전체 원소의 수가 2배가 되는 시점이므로, 이와 관련된 수라는게 직감적으로 와닿는다.
 
또 두번째 방법으로는  결론적인 것만 이해하는 거다. 
아무튼 간에 내가 구하고 싶은 bk 는 bk 를 구하면 b(k-1) 보다 크고 b(k) 와 같은 값들을 모두 삽입정렬에 이용해버릴 건데, 그 이유는 어차피 탐색횟수가 동일한 애들이기 때문이다. 
즉 b(k-1) +  1 ~ b(k) 는 탐색횟수가 동일한 인덱스 들이다. 
 
그리고 이진탐색에서 2^k개의 원소가 있을 떄 탐색 횟수는 k번이고 2^(k+1) -1 개일 때까지와 모두 동일하게 k번이다. 
 
 
mainChain으로 돌아가서, 
(k-1)번째로 넣으려는 원소가 있을 때 탐색대상인 전체 원소의 수가 아래와 같은데, 
 
 

 
 

 
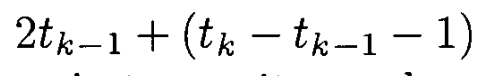
이 값이 2 ^ (k -1)일 때가 최대한으로 동일한 탐색횟수를 가지는 순간이므로, 등식을 사용해서 tk 에 대한 식을 구하면 

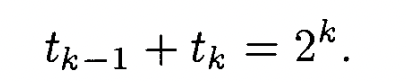
이 식이 나온다. 

 

 

다시 정리

마지막으로 정리하면,  (이것만 봐도 구현은 할 수 있다 ㅋㅋ)
 
먼저 쌍으로 나눈 뒤 더 큰 수를 ak, 작은 수를 bk로 두고 쌍을 정렬한다. 
이렇게 a는 정렬이 되어있고 b는 그냥 같은 위치의 a에 대해 더 작다는 것 빼고는 아무것도 모르는 상태에서
 

 
jacobsthal number에 의해서
이 순서대로 윗줄에 삽입정렬, 그것도 이진탐색방식으로 삽입정렬된다고 이해하면 된다. 
 
그래서 pending_elements인 bk 를 mainChain에 삽입 정렬을 할때 그 순서가 이렇게 된다는 것이다. 
 (괄호 안의 첫 숫자가 Jacobsthal number임을 확인하자)
1, (3, 2), (5, 4) , (11, 10, 9, 8, 7, 6), (21, 20, ... 12)

 

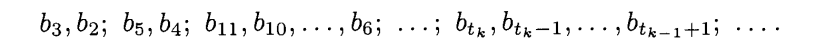
이진탐색 방식이기 때문에 그 특징을 이용해서 jacobsthal number의 순서로 b수열을 삽입정렬을 함으로써 비교하는 횟수를 최소한으로 만든 알고리즘이다.  (딱 떨어지는 알고리즘 이라기보다는 시나리오에 맞춘 알고리즘이다.  다른 알고리즘처럼  자세히 이해하려고 할 수록 답답했었는데 그 이유를 이제 알았다. )
 

 

※ 참고 사항

- 자세히 보면 도출한 tk식과 Jacobsthal number 식이 동일하지 않다.

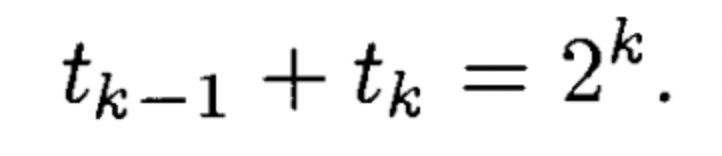
이항해서 넘겨봐도 다르다.. 충격...  
우선 수학적으로 둘이 같다고 증명이 바로 가능하진 않은 것 같다. 
다만 참고한 교과서에서는 t(0) = 1로 두고 Jacobsthal number는 J(0) = 0으로 두는데,
이런 차이도 있고 k = 1부터는 값이 같아서 그냥 넘기려고 한다. 
 
애초에 tk + t(k-1) = 2^(k-1) 이라는 점화식이 원하는 점화식이고, 이 값이 jacobsthal number와 동일해서 이 식으로 이야기를 하는거지, jacobsthal number와 직접적인 상관관계는 없는 것으로 추측해보려고 한다.
 
(독자여러분께 더 생각할 거리를 남기며... 알게 되신다면 댓글 부탁드립니다. )
 
- Jacobsthal number는 recursive 하게 구할 수 있는데, 이에 의해서 Mergesort도 재귀인 만큼 sort 하는 과정에서 별도로 Jacobsthal numbers 를 구해서 직접 막 삽입하는 과정을 피하고 한번에 딱 되지 않을까 하는 기대감이 있었는데, 그런건 아니고 직접 bk의 인덱스를 구해서 직접 일일히 삽입해주는게 맞지 않나 생각하고 있다. 
 
- 그런 의미해서 merge insertion sort 를 단순히

void mergeinsertionsort(int low, int high){
	int mid = (low + high)/2;
	mergeinsertionSort(low, mid);
	mergeinsertionSort(mid+1, high);
	mergeUsingInsertion(low, high);
}

이렇게 병합할 때만 insertion 을 쓴다든지, 
 
insertion 과정에서 binarySearch를 사용하지 않는다든지하는 코드는 Ford-Johnson algorithm 이 아니지 않나하는 의견이다. 
 
 
다른 의견이 있거나 더 잘 알고 있는 분이 있다면 알려주신다면 기쁘게 들을 것 같습니다. 
 
그럼 구현해보러 이만.. 구현에 대한 힌트도 시간이 되면 다음 게시물에서 써보겠습니다. 
 
 
 
 

참고 사이트

https://codereview.stackexchange.com/questions/116367/ford-johnson-merge-insertion-sort

Ford-Johnson merge-insertion sort

the art of computer programming vol 3  -  5.3.1장 184쪽 Merge insertion (<<< 보는 것 강추)

 

 

여기 까지 봤는데도 main chain 에 b1, b2, b3... 순으로 이진탐색해서 삽입정렬을 하려는 분은 없기를 바라면서.. 

그럼 왜 Jacobsthal number를 따르게 되었나?  이해안되실때...

0. 마음을 차분히 가진다. (저도 이해하는데 이틀 밤낮 소요된 것 같습니다.)

 

1. 이진 탐색 방법을 다시 이해해본다. (그림 참고) 그림만 이해되어도 만족하고 넘어간다.  

2. ak > bk 이라는 점을 이용해서 bk를 이진 탐색으로 삽입할 때 탐색 대상의 범위가 ak 이전의 수들임을 이해한다.

3. 이진탐색 시 최대 탐색 횟수가, 원소가 2^K 개 일 떄 부터 2 ^ (K + 1 ) - 1 개 일 때 K회라는 것을 이해한다.

4. 그리고 다시 이 글을 읽어본다.  

5. the art of computer programming vol 3  -  5.3.1장 184쪽 Merge insertion 을 읽어본다.

6. 수학 잘하는 사람을 찾는다.  (전 아니라서 머리 좀 싸맸습니다.. )

7. 쉽고도 간단하게 재귀적으로 구현된 mergesort-insertion 사이트를 발견했습니다.  : 사이트  : rust 로 구현된 mergesort-insertion