최단경로를 다익스트라로 풀고 있을 때,
그 경로도 구해야 하는 경우가 있다.
(백준 #5719 거의 최단경로 문제, k번째 최단경로 등)
이럴 때는 어떻게 경로를 저장할 수 있는지 알아보았다.
다익스트라의 진행과정은 다음과 같다.
<dijkstra pseudo code>
1. distance[S] <- 0, Q.push(S, S.weight) { 시작점의 거리 0으로 두기. 그리고 우선순위큐에 push}
2.while(! Q.isEmpty()) {우선순위큐가 비어있지 않는 동안}
1. now <- Q에서 pop {방문할 노드를 큐에서 꺼낸다.}
2. for u in adj(now) : {now의 인접노드를 순회하기 시작한다. }
nextCost = u.weight + distance[now]
if(nextCost < distance[u]) {현재 저장되어 있는 u의 최단경로보다 now에서 u로 오는 경로가 더 짧다면 갱신}
distance[u] = nextCost
Q.push(u, u.weight) {Q에 u과 가중치를 push한다.}이를 보면 알 수 있듯이 다익스트라는 최단경로가 저장되어있는 배열이 있고
그 배열을 계속 갱신해나가면서 한 시작점에서부터 다른 모든 노드까지의 최단경로를 구할 수 있는 방법이다.
갱신방법은 임의의 u, d에 대해 시작점에서 u까지의 거리 + u에서 d까지의 거리와 시작점에서 d까지의 최단경로 중 작은 값으로 갱신하는 것이다.
graph에서 d로 갈 수 있는 u에 대해
distance[d] <- min(distance[d], distance[u] + length[u,v])
따라서 경로를 저장하는 코드도 둘 중 더 작은 값을 비교하는 곳에 위치해야할 것이다.
위의 코드에서 둘 중 더 작은 값이 결정되어 갱신되는 위치는 아래 코드이다.
if(nextCost < distance[u]) {현재 저장되어 있는 u의 최단경로보다 now에서 u로 오는 경로가 더 짧다면 갱신}
distance[u] = nextCost {distance 업데이트}
Q.push(u, u.weight) {Q에 u과 가중치를 push한다.}여기에서 노드를 저장해주면 최단경로를 찾을 수 있다.
그런데 어떤 노드를 저장해야할까?
여기서 고민이 되었었다.
만약 now에서 next를 저장한다고 생각하면 다음과 같은 그래프에서
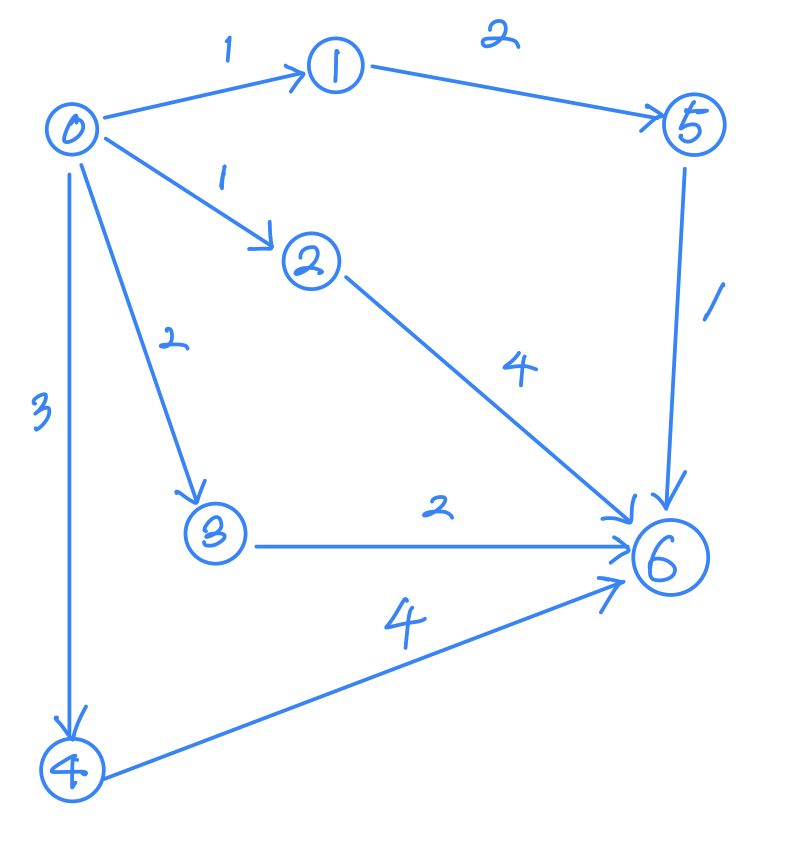
0 -> 1, 0->2, 0->3, 0->4 로 갈 때 모두 갱신이 되고, 모든 경로가 최단경로로써 저장이 될 것이다.
- 나중에 최단경로가 아님을 알고 지울 방법이 있는가?
-> 알수가 없다.
- 나중에 최단경로였음을 알고 되돌아 갈 수 있는 방법은?
-> 직전노드를 저장해준다면?
-> 갱신될 때마다 방문된 각 노드마다 직전노드를 저장한다면, 마지막에 종료되었을 때의 노드를 기준으로 직전노드로 되돌아가면(일명 벡트래킹) 그것이 최단경로일 것이다!
이러한 사고흐름을 통해, 최단경로의 실제 경로를 알기 위해서는 선임노드를 저장해주어야 함을 이해하고 있어야 한다.
이제 이해를 하였으니, 백준 5719번문제를 풀러 가보도록 하자.
https://ebang.tistory.com/71
백준 5719 - 거의 최단경로
문제 요즘 많은 자동차에서는 GPS 네비게이션 장비가 설치되어 있다. 네비게이션은 사용자가 입력한 출발점과 도착점 사이의 최단 경로를 검색해 준다. 하지만, 교통 상황을 고려하지 않고 최단
ebang.tistory.com
2023.05.04 수정버전 : 다익스트라인데 방문 확인 후 방문 하지 않은 노드만 방문하는 걸로 적어놨었다.
이런 말도 안되는 실수를 했음에 무한한 사과의 말씀을....
이는 절대 옳지 않고 다익스트라는 한번 방문했던 노드도 다시 방문가능하다.
그리고 가중치가 더 작은 업데이트 상황에서만 업데이트되고 큐에 푸쉬됨으로써 종료지점에 가까워진다!
'알고리즘 > 이론정리' 카테고리의 다른 글
| LIS - lower_bound 로 푸는 이유?(다이나믹 프로그래밍) (2) | 2023.02.21 |
|---|---|
| c++ 프로모션(연산 시 정수형, unsigned 변환) (0) | 2023.02.03 |
| 크루스칼 알고리즘 (1) | 2023.01.23 |
| 플로이드 워셜 알고리즘이란? - 원리를 바탕으로 (0) | 2023.01.22 |
| 유니온 파인드 (0) | 2023.01.21 |